Поиск
| Автор | Сообщение |
|---|---|
|
Robson
#
15 окт 2007 |
|
|
О.А.
#
16 окт 2007 |
|
|
Robson
#
17 окт 2007 |
|
|
О.А.
#
17 окт 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
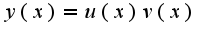 общее решение имеет вид
общее решение имеет вид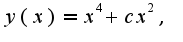 частное решение при начальном условии:
частное решение при начальном условии: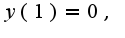 имеет вид
имеет вид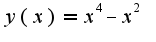 2)тоже линейное дифференциальное уравнение второго порядка, можно решить методом вариации произвольной константы, решение подобного уравнения можно найти в темах нашей консультации
2)тоже линейное дифференциальное уравнение второго порядка, можно решить методом вариации произвольной константы, решение подобного уравнения можно найти в темах нашей консультации
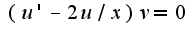 решением данного однородного уравнения является функция
решением данного однородного уравнения является функция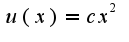 После предположения получим, что
После предположения получим, что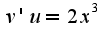 или
или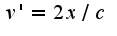 отсюда
отсюда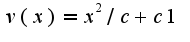 Перемножив
Перемножив