Форумы
>
Консультация по матанализу
>
Прошу помочь с производными, начинаю задание, но доделать не могу. Помогите
Поиск
| Автор | Сообщение |
|---|---|
|
Syrialilas
#
25 окт 2011 |
|
|
o_a
#
25 окт 2011 |
|
|
Syrialilas
#
26 окт 2011 |
|
|
o_a
#
26 окт 2011 |
|
|
Syrialilas
#
26 окт 2011 |
|
|
o_a
#
26 окт 2011 o_a
27 окт 2011
|
|
|
Syrialilas
#
27 окт 2011 |
Форумы
>
Консультация по матанализу
>
Прошу помочь с производными, начинаю задание, но доделать не могу. Помогите
Чтобы написать сообщение, необходимо войти или зарегистрироваться
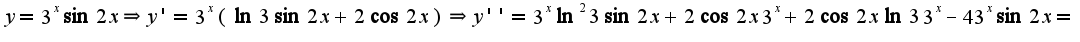
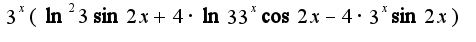
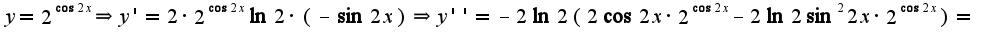
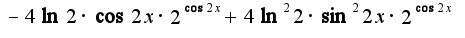
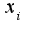 надо считать остальные переменные постоянными, поэтому в первом примере для нахождения производной по
надо считать остальные переменные постоянными, поэтому в первом примере для нахождения производной по  считаем
считаем 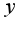 числом, получим
числом, получим 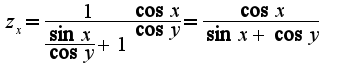 Совершенно аналогично,
Совершенно аналогично, 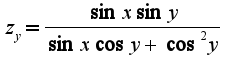 Что касается второго примера, то
Что касается второго примера, то 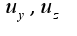 найдены правильно,
найдены правильно,