Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
Ольга
#
30 ноя 2009 |
|
|
О.А.
#
30 ноя 2009 |
|
|
Студент
#
1 дек 2009 |
|
|
Ольга
#
1 дек 2009 |
|
|
О.А.
#
1 дек 2009 |
|
|
Ольга
#
1 дек 2009 |
|
|
Студент
#
2 дек 2009 |
|
|
О.А.
#
2 дек 2009 |
|
|
Andrej
#
2 дек 2009 |
|
|
О.А.
#
2 дек 2009 |
|
|
Andrej
#
2 дек 2009 |
|
|
Олег
#
2 дек 2009 |
|
|
О.А.
#
2 дек 2009 |
|
|
NataliOo
#
3 дек 2009 |
|
|
Люба
#
3 дек 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
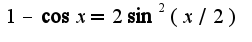 затем сведение ко второму замечательному пределу
затем сведение ко второму замечательному пределу
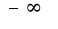 2)
2)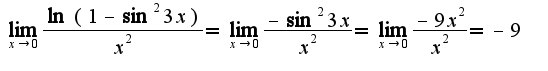 использованы асимптотические равенства
использованы асимптотические равенства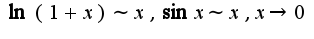
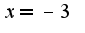 , во-вторых, сделайте замену
, во-вторых, сделайте замену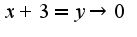 , тогда сведете ко второму замечательному пределу
, тогда сведете ко второму замечательному пределу