| Автор | Сообщение |
|---|---|
|
Саша
#
3 апр 2009 |
|
|
О.А.
#
4 апр 2009 |
|
|
Саша
#
4 апр 2009 |
|
|
Катя
#
5 апр 2009 |
|
|
Екатерина
#
7 апр 2009 |
|
|
О.А.
#
7 апр 2009 |
|
|
Екатерина
#
7 апр 2009 |
|
|
О.А.
#
7 апр 2009 |
|
|
Екатерина
#
7 апр 2009 |
|
|
О.А.
#
7 апр 2009 |
|
|
Екатерина
#
7 апр 2009 |
|
|
О.А.
#
7 апр 2009 |
|
|
ABTOPuTET
#
8 апр 2009 |
|
|
О.А.
#
8 апр 2009 |
|
|
Екатерина
#
8 апр 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
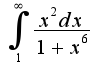
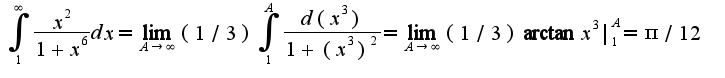
 подинтегральное выражение определено при
подинтегральное выражение определено при 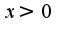 уточните задание(нижний предел), скорее всего это 3
уточните задание(нижний предел), скорее всего это 3
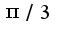
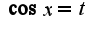 поэтому
поэтому