Поиск
Эльвира
#
11 ноя 2009
|
Здравствуйте! Проверьте, пожалуйста, исследование функции y=(x^2)/(x-1)
1. Область определения (-бесконечность;1)u(1;+бесконечность)
2. Функция ни четна, ни не четна
3. Вертикальная асимптота x=1
4. Наклонная асимптота y=x+1
5. y'=(x*(x-2))/(x-1)^2
Так как на интервале (-бесконечность;0)u(2;+бесконечность) производная положительна, то на указанных интервалах график функции возрастает.
Так как на интервале (0;1)u(1;2) производная отрицательна, то на указанных интервалах график функции убывает.
х=2 - точка локального максимума
х=0 - точка локального минимума
6. y''=2/(x-1)^3
Так как в интервале (-бесконечность;1)вторая производная отрицательна, то в указанном интервале график функции является выпуклым вверх.
Так как в интервале (1;+бесконечность)вторая производная положительна, то в указанном интервале график функции является выпуклым вниз (вогнутым).
7.График проходит через начало координат.
|
О.А.
#
11 ноя 2009
|
все правильно, за исключением точек экстремума, а именно, 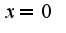 -максимум, 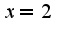 -минимум
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
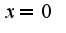 -максимум,
-максимум, 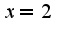 -минимум
-минимум