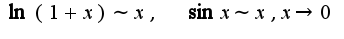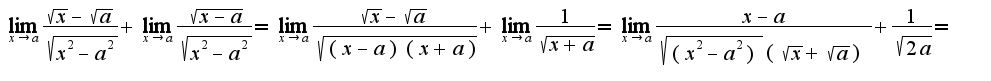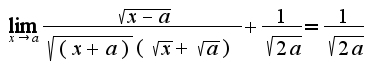Поиск
| Автор | Сообщение |
|---|---|
|
SrPomidoro
#
5 ноя 2014 |
|
|
o_a
#
5 ноя 2014 |
|
|
SrPomidoro
#
6 ноя 2014 |
|
|
o_a
#
6 ноя 2014 |
|
|
SrPomidoro
#
6 ноя 2014 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
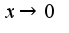 , а не
, а не 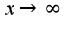 Для решения используется известная формула
Для решения используется известная формула 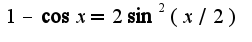 Поэтому
Поэтому 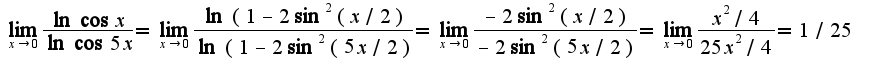 Использованы асимптотические равенства
Использованы асимптотические равенства