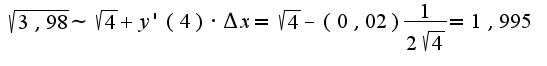Поиск
| Автор | Сообщение |
|---|---|
|
Учащийся Гр. 2111
#
17 дек 2007 |
|
|
О.А.
#
17 дек 2007 |
|
|
Учащийся Гр. 2111
#
17 дек 2007 |
|
|
О.А.
#
17 дек 2007 |
|
|
Учащийся Гр. 2111
#
17 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
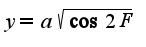 ,
,![${F\in[0,Pi/4]}$ ${F\in[0,Pi/4]}$](http://teacode.com/service/latex/latex.png?latex=%7BF%5Cin%5B0%2CPi%2F4%5D%7D&fontsize=21) Видимо я что-то не дописал, а что требуется найти?
2.
Видимо я что-то не дописал, а что требуется найти?
2.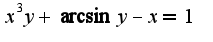 Тут требуется найти двойную производную в точке 1.1?
3.Вычислить
Тут требуется найти двойную производную в точке 1.1?
3.Вычислить 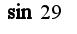 и
и 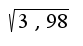 . Видимо это надо делать по формуле Маклерена, однако что в ней является показателем стрепени
. Видимо это надо делать по формуле Маклерена, однако что в ней является показателем стрепени 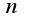 ?
?
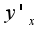 , которая задана в полярной системе координат
, которая задана в полярной системе координат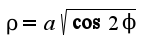 , при этом надо учесть формулы, связывающие полярную систему и декартову:
, при этом надо учесть формулы, связывающие полярную систему и декартову: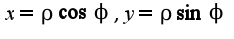 2)надо найти производную второго порядка от неявнозаданной функции и посчитать ее в указанной точке
3)для приближенного вычисления надо использовать понятие дифференциала функции и формулу, связывающую приращение и дифференциал
2)надо найти производную второго порядка от неявнозаданной функции и посчитать ее в указанной точке
3)для приближенного вычисления надо использовать понятие дифференциала функции и формулу, связывающую приращение и дифференциал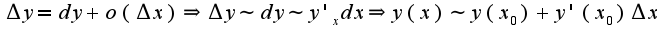
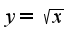 при
при 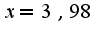 пользуемся указанной формулой
пользуемся указанной формулой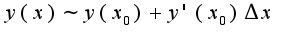 Выбираем в качестве
Выбираем в качестве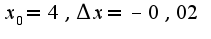 Тогда
Тогда