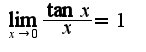Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Поиск| Автор | Сообщение |
|---|---|
|
marisoll
#
18 мар 2009 |
|
|
О.А.
#
18 мар 2009 |
|
|
Человек, который не знает
#
19 мар 2009 |
|
|
О.А.
#
19 мар 2009 |
|
|
Денис
#
19 мар 2009 |
|
|
О.А.
#
19 мар 2009 |
|
|
Денис
#
19 мар 2009 |
|
|
О.А.
#
19 мар 2009 |
|
|
Денис
#
20 мар 2009 |
|
|
Человек, который не знает
#
24 мар 2009 |
|
|
О.А.
#
24 мар 2009 |
|
|
Темный Иной
#
25 мар 2009 |
|
|
О.А.
#
25 мар 2009 |
|
|
Ника
#
30 мар 2009 |
|
|
О.А.
#
30 мар 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

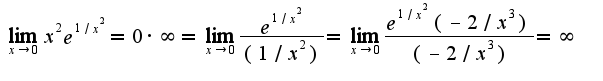
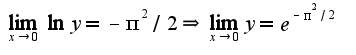 2)
2)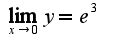 3
3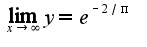
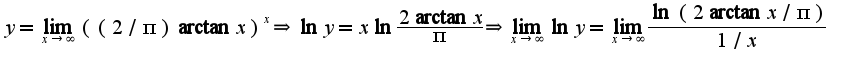
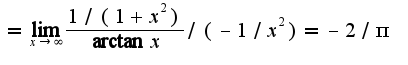
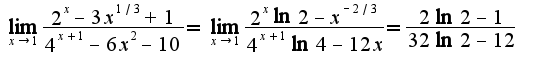
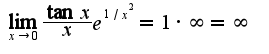 следствие из первого замечательного предела
следствие из первого замечательного предела