Поиск
| Автор | Сообщение |
|---|---|
|
sv21
#
13 ноя 2013 |
|
|
o.a.
#
13 ноя 2013 |
|
|
sv21
#
13 ноя 2013 |
|
|
o.a.
#
13 ноя 2013 |
|
|
sv21
#
13 ноя 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
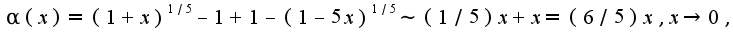 то есть
то есть 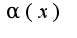 - первого порядка малости
2)
- первого порядка малости
2)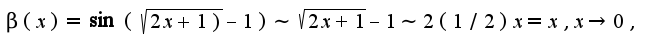 то есть
то есть 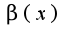 - первого порядка малости. Использованы известные асимптотические равенства
- первого порядка малости. Использованы известные асимптотические равенства 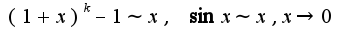
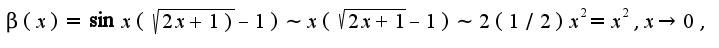 то есть
то есть