Поиск
| Автор | Сообщение |
|---|---|
|
Евгения
#
22 ноя 2008 |
|
|
О.А.
#
22 ноя 2008 |
|
|
Евгения
#
22 ноя 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
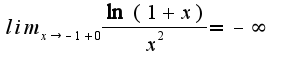 , для левосторонней окрестности точки минус единица функция неопределена, поэтому не надо находить предел слева в этой точке, точка минус единица тоже является разрывом второго рода
, для левосторонней окрестности точки минус единица функция неопределена, поэтому не надо находить предел слева в этой точке, точка минус единица тоже является разрывом второго рода