Поиск
| Автор | Сообщение |
|---|---|
|
pearl_girl
#
2 дек 2008 |
|
|
О.А.
#
2 дек 2008 |
|
|
pearl_girl
#
3 дек 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
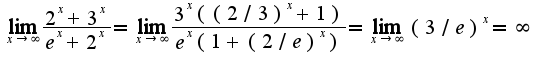 2)сделайте замену
2)сделайте замену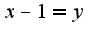 , затем используйте известные пределы
, затем используйте известные пределы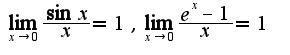 3)примените второй замечательный предел
3)примените второй замечательный предел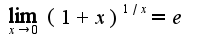 4)ответ правильный
4)ответ правильный