Поиск
Саша
#
15 янв 2009
|
Здравствуйте! Помогите пожалуйста с пределом, никак не получается прийти к ответу 2/3 уже замучался.
lim n^2 *((5+n^3)^(1/3)-(3+n^3)^1/3)
n к бесконечности
Я пытался делить и домножать на (5+n^3)^(2/3) +(5+n^3)^(1/3)*(3+n^3)^(1/3) + (3+n^3)^2/3
После преобразованией получилось n^(2) *(2n^(3) +8)
В знаменателе вынес n^2, и сократил с n^2 в числителе, а дальше, что делать не знаю.
И еще один предел
lim(1+1/3 + 1/3^2 + ...+1/3^n)/(1+1/5 +1/5^2 + ...+1/5^n)
n к бесконечности
Здесь же вроде сначала нужно написать формулу для последовательности, но я что - то ни как не придумаю какую
|
О.А.
#
15 янв 2009
|
здравствуйте.
Вы правильно начали делать в первом примере, действительно, надо умножить и разделить выражение на 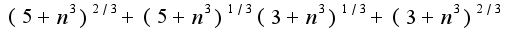 , затем использовать формулу 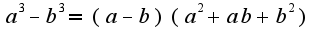 , поэтому после упрощений получается следующее выражение 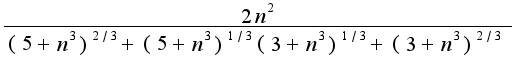 Затем в знаменателе выносится 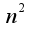 , и нужно сократить дробь на 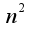 ,в результате в пределе получается 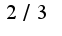
В0 втором примере используется формула суммы геометрической прогрессии 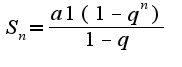 Т.е. 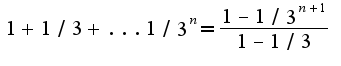 Аналогично, 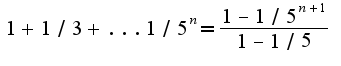 переходя к пределу, получим 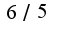
|
Саша
#
15 янв 2009
|
Спасибо большое, разобрался, когда в числителе раскрывал скобки знак минус потерял и поэтому получил такой результат в числителе
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
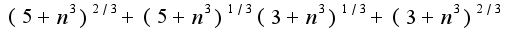 , затем использовать формулу
, затем использовать формулу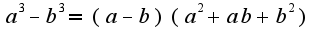 , поэтому после упрощений получается следующее выражение
, поэтому после упрощений получается следующее выражение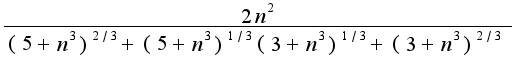 Затем в знаменателе выносится
Затем в знаменателе выносится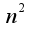 , и нужно сократить дробь на
, и нужно сократить дробь на 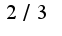 В0 втором примере используется формула суммы геометрической прогрессии
В0 втором примере используется формула суммы геометрической прогрессии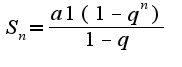 Т.е.
Т.е.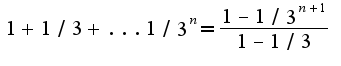 Аналогично,
Аналогично,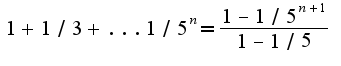 переходя к пределу, получим
переходя к пределу, получим