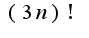ряд

Форумы > Консультация по матанализу > ряд

Автор	Сообщение
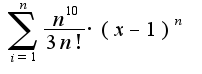Настенька # 1 дек 0707	Здравствуйте, Ольга Александровна, помогите найти радиус и область сходимости степенного ряда, $\sum_{i=1}^{n}{\frac {n^{10} } {3n!}\cdot (x-1)^n}$ что то я даже незнаю с чего начать, при попытке найти радиус по признаку Даламбера, получается 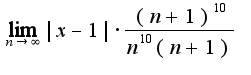$\lim_{n \to \infty}{\|x-1\| \cdot \frac {(n+1)^{10}}{n^{10}(n+1)}}$ а как дальше?
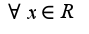О.А. # сегодня в 22:37	здравствуйте, согласно признаку Даламбера предел должен быть меньше единицы для сходимости ряда, т.к. для данного примера предел равен нулю, то область сходимости вся числовая ось,т.е $\forall x\in R$ ряд сходится, кроме того, для нахождения радиуса сходимости можно было использовать формулу 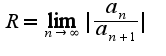$R=\lim_{n\rightarrow \infty}\|\frac{a_{n}}{a_{n+1}}\|$ . результат получится тот же 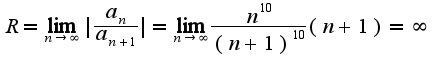$R=\lim_{n\rightarrow \infty}\|\frac{a_{n}}{a_{n+1}}\|=\lim_{n\rightarrow \infty}\frac{n^10}{(n+1)^{10}}(n+1)=\infty$ ,все рассуждения приведены для варианта 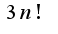$3n!$ ,который отличается от следующего $(3n)!$
Настенька # 14 ноя 2008	оказалось всё просто, а в методичке в примере что-то так много было написано, исследовали на границах потом ещё... тут всё понятно, Спасибо Вам огромное!
Ваш ответ:	Чтобы написать сообщение, необходимо войти или зарегистрироваться

Форумы > Консультация по матанализу > ряд

Чтобы написать сообщение, необходимо войти или зарегистрироваться