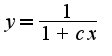Поиск
Стася
#
10 апр 2008
|
1. Исследовать на сходимость числовой ряд
а) Summ (беск.,n=1) (n2^n/5^n)
Исследуем по признаку Даламбера:
lim(nстремиться к беск.) (n+1)2^n+1*5^n/5^n+1*n2^n)= lim(nстремиться к беск.)(n+1/n)= lim(nстремиться к беск.)(1+1/n)=0. Следовательно ряды сходятся.
б) Summ (беск.,n=1) (sinn/n^2)
Решаем с помощью 2-ого признака сравнения
Unстремится к 0,
Vn=1/n^2,
lim(nстремиться к беск.)((sinn*n^2)/n^2*1)= lim(nстремиться к беск.)sinn= 1/2=0,5.
Согласно 2-му признаку сходится.
2.Найти область сходимости степенного ряда.
Summ(беск.,n=1) ((n/n^3+1)*(x+3)^n)
1) R = lim (n*(n^3+1)/(n^3+1)*(n+1))= (n/n+1)=(1/1+1/n)=1,
2) -1<x+3<1
-4<x<-2
3.Найти частное решение диф.уравнения
xy'+y=y^2 y(1)=1/2
Решаем методом Бернули:
Делим обе части на y^2
(x/y^2)*y'+(1/y)=1, делаем замену
z=1/y=y^(-1)
z'=1/y^2-y'
z'x+z=1, делим на x
z'+(z/x)=1/x
Делаем:
z=uv
z'=u'v+uv', следовательно
u'v+uv'+(uv/x)=1/x
u'v+u(v'+(v/x))=1/x
a) v'+(v/x)=0
v=1/x
b) u'(1/x)=1/x
u'=0
u=c
z=uv,значит z=c*x^-1
1/y=c*(1/x)
Частное решение:
y=1/2
x=1
Подставляем:
(1/(1/2))=c/1
c=2, следовательно y=2*x^-1
это и есть частное решение.
|
О.А.
#
10 апр 2008
|
1) предел найден неверно
2)нужно использовать признак сравнения 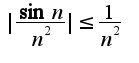 известно, что ряд 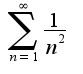 -сходится, поэтому исходный ряд сходится
3)радиус найден правильно, но решение неверно
4) метод решения выбран правильный, но результат неверный,общее решение данного уравнения имеет вид 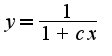
|
Настя
#
14 апр 2008
|
Проверьте производные пожалуйста
y=(2x^3+x)ctg3x
y'=(2x^2+x)'ctg3x+(ctg3x)'(2x^3+x)=(6x^2+1)ctg3x- 6x^3+3x/sin^2 3x
|
О.А.
#
14 апр 2008
|
общий минус стоит перед вторым слагаемым
|
Ваш ответ:
|
|
Чтобы написать сообщение, необходимо войти или зарегистрироваться
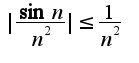 известно, что ряд
известно, что ряд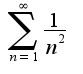 -сходится, поэтому исходный ряд сходится
3)радиус найден правильно, но решение неверно
4) метод решения выбран правильный, но результат неверный,общее решение данного уравнения имеет вид
-сходится, поэтому исходный ряд сходится
3)радиус найден правильно, но решение неверно
4) метод решения выбран правильный, но результат неверный,общее решение данного уравнения имеет вид