| Автор | Сообщение |
|---|---|
|
Ольга
#
12 апр 2009 |
|
|
О.А.
#
12 апр 2009 |
|
|
Катя
#
15 апр 2009 |
|
|
Катя
#
15 апр 2009 |
|
|
О.А.
#
15 апр 2009 |
|
|
Екатерина
#
16 апр 2009 |
|
|
О.А.
#
16 апр 2009 |
|
|
Екатерина
#
17 апр 2009 |
|
|
О.А.
#
17 апр 2009 |
|
|
Екатерина
#
17 апр 2009 |
|
|
О.А.
#
17 апр 2009 |
|
|
PreF
#
22 мая 2011 |
|
|
o_a
#
23 мая 2011 |
|
|
PreF
#
23 мая 2011 |
|
|
o_a
#
23 мая 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
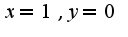 график выпуклый вверх везде в области определения, остальное правильно
график выпуклый вверх везде в области определения, остальное правильно
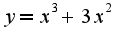 имеет координаты
имеет координаты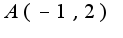 других нет, в начале координат-минимум,
интервалы выпуклости определены правильно
других нет, в начале координат-минимум,
интервалы выпуклости определены правильно
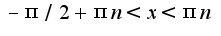
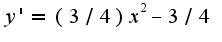 ирассмотрите при каких
ирассмотрите при каких  она меньше(убывает) и больше нуля(возрастает). Для нахождения экстремума используйте первую производную(первое достаточное условие существование экстремума). Данная функция имеет минимум при
она меньше(убывает) и больше нуля(возрастает). Для нахождения экстремума используйте первую производную(первое достаточное условие существование экстремума). Данная функция имеет минимум при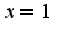 и максимум при
и максимум при 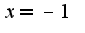 5) для нахождения точек перегиба найдите вторую производную и посмотрите меняет ли она знак при переходе через
5) для нахождения точек перегиба найдите вторую производную и посмотрите меняет ли она знак при переходе через 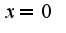 если меняет, то есть точка перегиба, в данном случае
если меняет, то есть точка перегиба, в данном случае 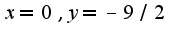 -точка перегиба
6) асимптот нет
-точка перегиба
6) асимптот нет