Поиск
| Автор | Сообщение |
|---|---|
|
Артур
#
10 мая 2020 |
|
|
o_a
#
12 мая 2020 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
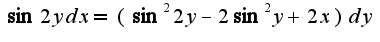 нужно записать уравнение в виде:
нужно записать уравнение в виде: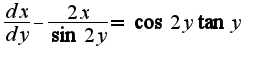 , которое является линейным уравнением и решается по стандартной схеме заменой
, которое является линейным уравнением и решается по стандартной схеме заменой