Поиск
| Автор | Сообщение |
|---|---|
|
Толик
#
26 апр 2007 |
|
|
О.А.
#
27 апр 2007 |
|
|
Виктор
#
4 июн 2009 |
|
|
О.А.
#
4 июн 2009 |
|
|
Виктор
#
4 июн 2009 |
|
|
О.А.
#
4 июн 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
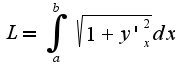 Для данной функции получается интеграл
Для данной функции получается интеграл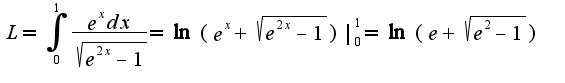
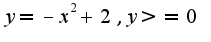 (больше либо равно)
(больше либо равно)
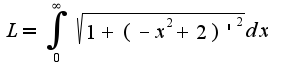 ?
?