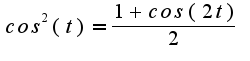Поиск
| Автор | Сообщение |
|---|---|
|
Елена
#
27 окт 2007 |
|
|
О.А.
#
27 окт 2007 |
|
|
Елена
#
28 окт 2007 |
|
|
О.А.
#
28 окт 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
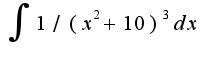 - нужно решать разложением на простейшие дроби.
2.
- нужно решать разложением на простейшие дроби.
2. 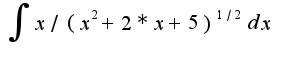 - выделяем в знаменателе полный квадрат
3.
- выделяем в знаменателе полный квадрат
3. 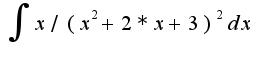 - выделяем в знаменателе полный квадрат
Спасибо.
- выделяем в знаменателе полный квадрат
Спасибо.
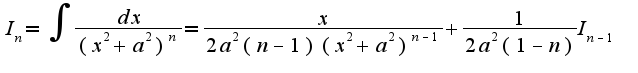 2),3)методы решения применимы
2),3)методы решения применимы
![$ {\int_{}^{}{\frac{dx}{(x^2+5)^3}}} = [{x=\sqrt{5}}tg(t) t=arctg(\frac{x}{\sqrt{5}}) dx={\frac{\sqrt{5}dt}{cos^2(t)}}] = {\int_{}^{}{\frac{\sqrt{5}dt}{cos^2(t)(5tg(t)+5)^3}}} = {\sqrt{5} {\int_{}^{}{\frac{dt}{cos^2(t)[5(tg^2(t)+1)]^3}}}} = {\frac{\sqrt{5}}{125}}{\int_{}^{}{\frac{dt}{\frac{cos^2(t)}{cos^6(t)}}}} = {\frac{\sqrt{5}}{125}}{\int_{}^{}{cos^4(t)dt}}$ $ {\int_{}^{}{\frac{dx}{(x^2+5)^3}}} = [{x=\sqrt{5}}tg(t) t=arctg(\frac{x}{\sqrt{5}}) dx={\frac{\sqrt{5}dt}{cos^2(t)}}] = {\int_{}^{}{\frac{\sqrt{5}dt}{cos^2(t)(5tg(t)+5)^3}}} = {\sqrt{5} {\int_{}^{}{\frac{dt}{cos^2(t)[5(tg^2(t)+1)]^3}}}} = {\frac{\sqrt{5}}{125}}{\int_{}^{}{\frac{dt}{\frac{cos^2(t)}{cos^6(t)}}}} = {\frac{\sqrt{5}}{125}}{\int_{}^{}{cos^4(t)dt}}$](http://teacode.com/service/latex/latex.png?latex=+%7B%5Cint_%7B%7D%5E%7B%7D%7B%5Cfrac%7Bdx%7D%7B%28x%5E2%2B5%29%5E3%7D%7D%7D+%3D+%5B%7Bx%3D%5Csqrt%7B5%7D%7Dtg%28t%29+++++++t%3Darctg%28%5Cfrac%7Bx%7D%7B%5Csqrt%7B5%7D%7D%29+++dx%3D%7B%5Cfrac%7B%5Csqrt%7B5%7Ddt%7D%7Bcos%5E2%28t%29%7D%7D%5D+%3D+%7B%5Cint_%7B%7D%5E%7B%7D%7B%5Cfrac%7B%5Csqrt%7B5%7Ddt%7D%7Bcos%5E2%28t%29%285tg%28t%29%2B5%29%5E3%7D%7D%7D+%3D+%7B%5Csqrt%7B5%7D+%7B%5Cint_%7B%7D%5E%7B%7D%7B%5Cfrac%7Bdt%7D%7Bcos%5E2%28t%29%5B5%28tg%5E2%28t%29%2B1%29%5D%5E3%7D%7D%7D%7D+%3D+%7B%5Cfrac%7B%5Csqrt%7B5%7D%7D%7B125%7D%7D%7B%5Cint_%7B%7D%5E%7B%7D%7B%5Cfrac%7Bdt%7D%7B%5Cfrac%7Bcos%5E2%28t%29%7D%7Bcos%5E6%28t%29%7D%7D%7D%7D+%3D+%7B%5Cfrac%7B%5Csqrt%7B5%7D%7D%7B125%7D%7D%7B%5Cint_%7B%7D%5E%7B%7D%7Bcos%5E4%28t%29dt%7D%7D&fontsize=21) Ну а дальше по формуле 2 раза понижаем степень косинуса:
Ну а дальше по формуле 2 раза понижаем степень косинуса: