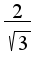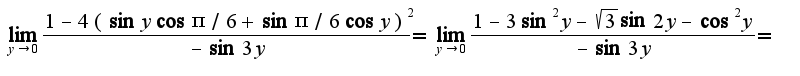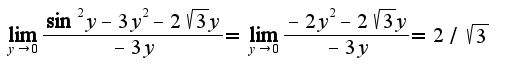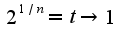Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
Alexx
#
22 дек 2012 |
|
|
CoH1K
#
26 дек 2012 |
|
|
CoH1K
#
26 дек 2012 |
|
|
megamenin
#
26 дек 2012 |
|
|
o_a
#
26 дек 2012 |
|
|
o_a
#
26 дек 2012 |
|
|
mkras
#
26 дек 2012 |
|
|
o_a
#
26 дек 2012 |
|
|
mkras
#
26 дек 2012 |
|
|
mkras
#
27 дек 2012 |
|
|
StudentVMK
#
27 дек 2012 |
|
|
o_a
#
27 дек 2012 |
|
|
o_a
#
27 дек 2012 |
|
|
mkras
#
28 дек 2012 |
|
|
kira
#
28 дек 2012 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
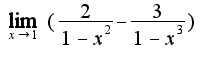 нужно привести к общему знаменателю, затем сократить на общий множитель
нужно привести к общему знаменателю, затем сократить на общий множитель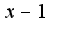 ответ
ответ 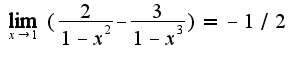
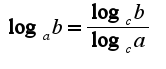 Прологарифмируйте функцию по основанию
Прологарифмируйте функцию по основанию 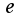 и найдите предел
и найдите предел
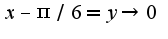 Затем использовать асимптотическое равенство
Затем использовать асимптотическое равенство 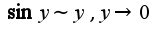 Ответ:
Ответ: