Поиск
| Автор | Сообщение |
|---|---|
|
Алексей
#
22 июн 2006 |
|
|
О.А.
#
24 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
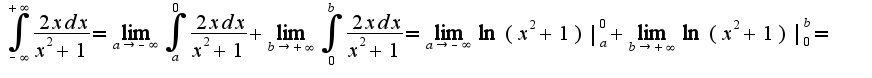
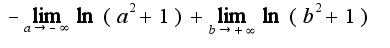 Т. е. данный интеграл расходится, однако, если вычислять главное значение данного интеграла, то оно равно нулю,т.к. по определению в этом случае
Т. е. данный интеграл расходится, однако, если вычислять главное значение данного интеграла, то оно равно нулю,т.к. по определению в этом случае 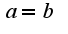 ,т.е
,т.е 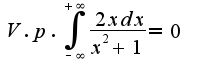 2) для вычисления площади используется стандартная формула
2) для вычисления площади используется стандартная формула 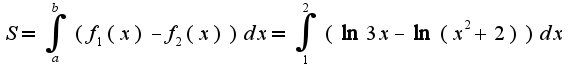 Для вычисления интеграла используется формула интегрирования по частям, поэтому окончательно получим:
Для вычисления интеграла используется формула интегрирования по частям, поэтому окончательно получим: