Поиск
| Автор | Сообщение |
|---|---|
|
Pantera
#
3 июн 2006 |
|
|
О.А.
#
5 июн 2006 |
|
|
Pantera
#
5 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
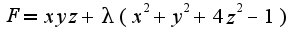 Затем находят производные по всем переменным, включая
Затем находят производные по всем переменным, включая 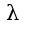 , и приравнивают нулю, чтобы найти стационарные точки, присоединяют урвнение связи:
, и приравнивают нулю, чтобы найти стационарные точки, присоединяют урвнение связи: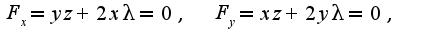
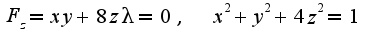 Решением
данной системы уравнений является точка A
Решением
данной системы уравнений является точка A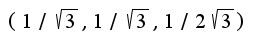 Значение
Значение 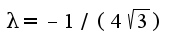 Чтобы узнать есть ли экстремум в найденной точке, надо определить знак у второго дифференциала от функции Лагранжа. Для этого находят производные второго порядка от F:
Чтобы узнать есть ли экстремум в найденной точке, надо определить знак у второго дифференциала от функции Лагранжа. Для этого находят производные второго порядка от F: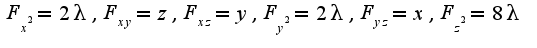 Подставляя в найденные производные точку
Подставляя в найденные производные точку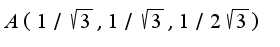 , учитывая, что
, учитывая, что 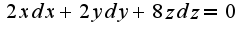 , нужно все это подставить в формулу для второго дифференциала
, нужно все это подставить в формулу для второго дифференциала 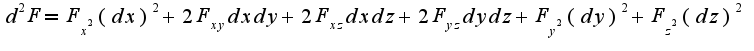 Нетрудно поверить, что знак
Нетрудно поверить, что знак 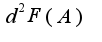 получается отрицательный, т.е в точке A -максимум.
получается отрицательный, т.е в точке A -максимум.