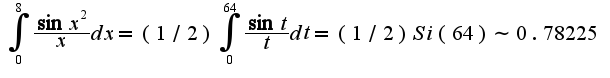| Автор | Сообщение |
|---|---|
|
Оленька
#
17 апр 2011 |
|
|
o_a
#
17 апр 2011 |
|
|
Liza_Nikitina
#
29 апр 2011 |
|
|
o_a
#
29 апр 2011 |
|
|
bekzod1092
#
22 мая 2011 |
|
|
o_a
#
22 мая 2011 |
|
|
Fier
#
24 мая 2011 |
|
|
o_a
#
24 мая 2011 |
|
|
Fier
#
24 мая 2011 |
|
|
o_a
#
24 мая 2011 |
|
|
Fier
#
24 мая 2011 |
|
|
НАТА
#
26 мая 2011 |
|
|
o_a
#
26 мая 2011 |
|
|
Тара
#
13 июн 2011 |
|
|
o_a
#
13 июн 2011 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
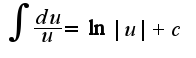 надо иметь в числителе дроби дифференциал знаменателя, то есть
надо иметь в числителе дроби дифференциал знаменателя, то есть 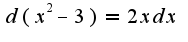 А в данном интеграле в числителе находится выражение
А в данном интеграле в числителе находится выражение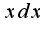 , поэтому домножаем на 2 и делим на 2, чтобы выражение не изменилось, сл-но,
, поэтому домножаем на 2 и делим на 2, чтобы выражение не изменилось, сл-но, 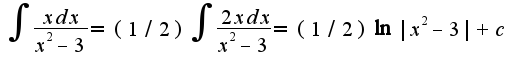
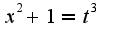 поскольку выражение под интегралом-дифференциальный бином, ответ
поскольку выражение под интегралом-дифференциальный бином, ответ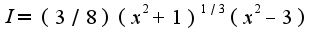
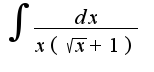 то замена
то замена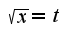 2) замена
2) замена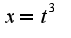
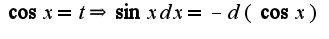
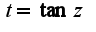 интегрируйте по частям
интегрируйте по частям 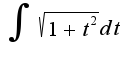
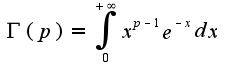 называется гамма функцией от
называется гамма функцией от 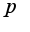 и сходится при
и сходится при 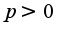 ,чтобы свести к указанному интегралу
,чтобы свести к указанному интегралу 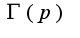 надо сделать замену в данном интеграле
надо сделать замену в данном интеграле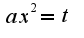
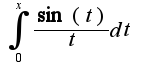 называется интегральным синусом, для его вычисления составлены таблицы
называется интегральным синусом, для его вычисления составлены таблицы