Форумы
>
Консультация по матанализу
>
помогите разобраться с нахождением предела по правилу лопиталя
Поиск
| Автор | Сообщение |
|---|---|
|
owl
#
20 янв 2012 owl
20 янв 2012
|
|
|
o_a
#
20 янв 2012 |
|
|
owl
#
20 янв 2012 |
|
|
owl
#
21 янв 2012 |
|
|
o_a
#
21 янв 2012 |
|
|
owl
#
21 янв 2012 |
|
|
o_a
#
22 янв 2012 |
|
|
owl
#
29 янв 2012 owl
29 янв 2012
|
|
|
o_a
#
29 янв 2012 |
Форумы
>
Консультация по матанализу
>
помогите разобраться с нахождением предела по правилу лопиталя
Чтобы написать сообщение, необходимо войти или зарегистрироваться
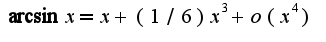 Сл-но,
Сл-но, 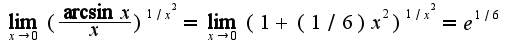
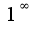 -неопределенность. Чтобы найти предел от данной функции надо применить правило Лопиталя дважды,
-неопределенность. Чтобы найти предел от данной функции надо применить правило Лопиталя дважды, 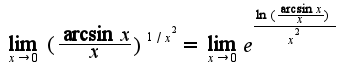
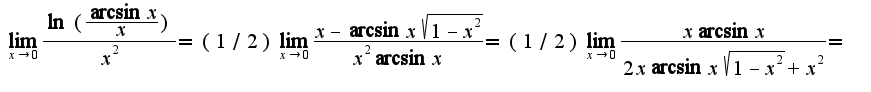
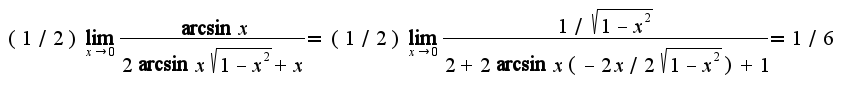 Сл-но, предел равен
Сл-но, предел равен 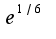
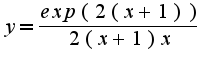 имеет вид, откуда следует, что предел слева при
имеет вид, откуда следует, что предел слева при 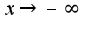 равен нулю, а предел справа равен бесконечности
равен нулю, а предел справа равен бесконечности
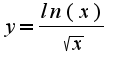 1)
1)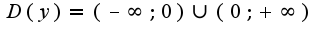 2)c OX:(1;0)
с осью OY не пересекается
3)ни чётная ,ни нечётная
4) a)
2)c OX:(1;0)
с осью OY не пересекается
3)ни чётная ,ни нечётная
4) a)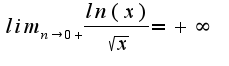
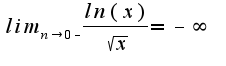 x=0-вертикальная асимптота
б)k=
x=0-вертикальная асимптота
б)k=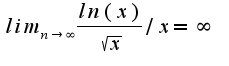 значит наклонная и горизонтальная асимптоты отсутствуют
5)
значит наклонная и горизонтальная асимптоты отсутствуют
5)![$f'(x)=\frac{2-ln(x)}{\sqrt[2]{2x^3}}$ $f'(x)=\frac{2-ln(x)}{\sqrt[2]{2x^3}}$](http://teacode.com/service/latex/latex.png?latex=f%27%28x%29%3D%5Cfrac%7B2-ln%28x%29%7D%7B%5Csqrt%5B2%5D%7B2x%5E3%7D%7D&fontsize=21) x=e^2 f(x)
x=e^2 f(x) 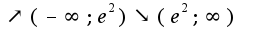 min=(e^2;2/e)
6)
min=(e^2;2/e)
6)![$f ''(x)=\frac{3ln(x)-8}{\sqrt[2]{4x^5}}$ $f ''(x)=\frac{3ln(x)-8}{\sqrt[2]{4x^5}}$](http://teacode.com/service/latex/latex.png?latex=f+%27%27%28x%29%3D%5Cfrac%7B3ln%28x%29-8%7D%7B%5Csqrt%5B2%5D%7B4x%5E5%7D%7D&fontsize=21) x=e^(8/3) выпукла
x=e^(8/3) выпукла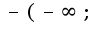 e^(8/3)),вогнута-(e^(8/3);+infty)
правильно ли посчитал k?
e^(8/3)),вогнута-(e^(8/3);+infty)
правильно ли посчитал k?
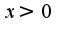 из-за функции логарифма, кроме того, наличия корня, поэтому область определения
из-за функции логарифма, кроме того, наличия корня, поэтому область определения 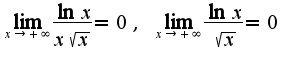 Поэтому существует горизонтальная асимптота
Поэтому существует горизонтальная асимптота 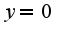 производная найдена верно, а вот в точке
производная найдена верно, а вот в точке 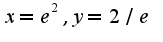 максимум, а не минимум, как у вас написано. При
максимум, а не минимум, как у вас написано. При 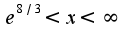 функция выпукла вниз, а при
функция выпукла вниз, а при 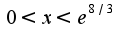 -выпукла вверх. В пункте 4 написанного исследования неверно указаны предельные точки надо
-выпукла вверх. В пункте 4 написанного исследования неверно указаны предельные точки надо