Поиск
| Автор | Сообщение |
|---|---|
|
Pantera
#
17 апр 2006 |
|
|
О.А.
#
18 апр 2006 |
|
|
Pantera
#
18 апр 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
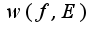 функции f(x) на множестве E называется
функции f(x) на множестве E называется
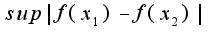 по всем
по всем 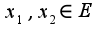 . Колебанием функции f(x) в точке a называется
. Колебанием функции f(x) в точке a называется 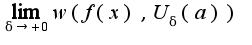 ,где
,где 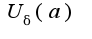 -
-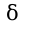 -окрестность точки a.Справедлив критерий Коши: существует предел функции
-окрестность точки a.Справедлив критерий Коши: существует предел функции 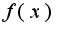 по базе
по базе 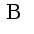 тогда и только тогда, когда для любого положит.
тогда и только тогда, когда для любого положит. 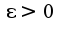 найдется элемент базы, на котором колебание функции меньше
найдется элемент базы, на котором колебание функции меньше 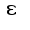 .
.