Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
Лена
#
8 ноя 2006 |
|
|
О.А.
#
8 ноя 2006 |
|
|
лена
#
9 ноя 2006 |
|
|
PredatoR_GH
#
7 янв 2007 |
|
|
О.А.
#
7 янв 2007 |
|
|
PredatoR_GH
#
8 янв 2007 |
|
|
О.А.
#
8 янв 2007 |
|
|
PredatoR_GH
#
8 янв 2007 |
|
|
PredatoR_GH
#
14 янв 2007 |
|
|
О.А.
#
14 янв 2007 |
|
|
Наташа
#
29 дек 2007 |
|
|
О.А.
#
29 дек 2007 |
|
|
A440
#
2 апр 2008 |
|
|
О.А.
#
2 апр 2008 |
|
|
Александр
#
3 апр 2008 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
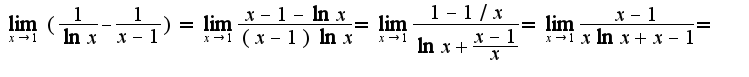
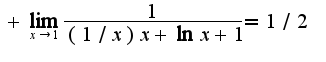
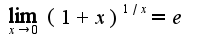
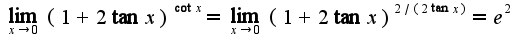
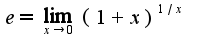 и
и 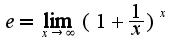 Сомнений в правильности решения данного примера у меня нет, а вам совет-больше читайте учебники!
Сомнений в правильности решения данного примера у меня нет, а вам совет-больше читайте учебники!
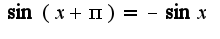 Кроме того, известны асимптотические формулы:
Кроме того, известны асимптотические формулы: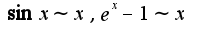 при
при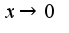 Поэтому предел равен нулю.
2) надо сравнить наивысшие степени от x в числителе и знаменателе
Поэтому предел равен нулю.
2) надо сравнить наивысшие степени от x в числителе и знаменателе
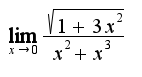 , или в числителе еще минус единица?
, или в числителе еще минус единица?