Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Поиск| Автор | Сообщение |
|---|---|
|
paulinio
#
14 дек 2011 |
|
|
o_a
#
14 дек 2011 |
|
|
paulinio
#
14 дек 2011 |
|
|
o_a
#
14 дек 2011 |
|
|
paulinio
#
14 дек 2011 |
|
|
paulinio
#
15 дек 2011 |
|
|
o_a
#
15 дек 2011 |
|
|
hayley
#
28 дек 2011 |
|
|
o_a
#
28 дек 2011 |
|
|
Малинка
#
28 дек 2011 |
|
|
o_a
#
28 дек 2011 |
|
|
анастэйшн
#
29 дек 2011 |
|
|
o_a
#
29 дек 2011 |
|
|
kisskiss1232009
#
17 фев 2012 |
|
|
o_a
#
17 фев 2012 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
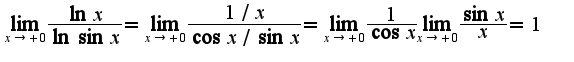
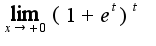 , а что делать дальше? прологарифмировать?или свести к замечательному пределу?
2.не подскажите ход решения 17.54?
, а что делать дальше? прологарифмировать?или свести к замечательному пределу?
2.не подскажите ход решения 17.54?
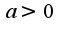 и
и 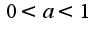
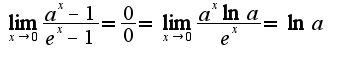
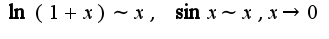
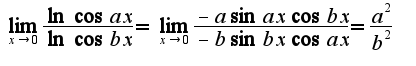 при решении кроме правила Лопиталя используется первый замечательный предел
при решении кроме правила Лопиталя используется первый замечательный предел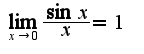 2)
2)