Поиск
| Автор | Сообщение |
|---|---|
|
Ольга
#
15 дек 2013 |
|
|
o_a
#
15 дек 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
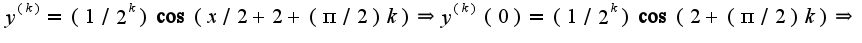
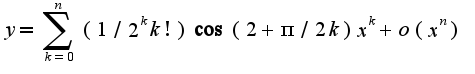 2)предварительно представить дробь в виде разности двух дробей:
2)предварительно представить дробь в виде разности двух дробей: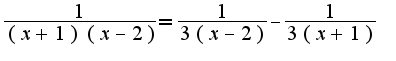 Затем использовать известное разложение, которое изучалось на практике:
Затем использовать известное разложение, которое изучалось на практике: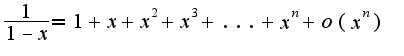 (сумма геометрической прогрессии)
(сумма геометрической прогрессии)