Поиск
| Автор | Сообщение |
|---|---|
|
HK
#
16 июн 2008 |
|
|
Настена
#
16 июн 2008 |
|
|
О.А.
#
16 июн 2008 |
|
|
HK
#
17 июн 2008 |
|
|
Настена
#
17 июн 2008 |
|
|
HK
#
19 июн 2008 |
|
|
О.А.
#
19 июн 2008 |
|
|
HK
#
19 июн 2008 |
|
|
Hagen
#
25 сен 2008 |
|
|
О.А.
#
29 сен 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
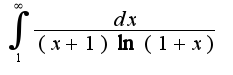 )Поскольку интеграл расходится, то и расходится указанный ряд
Что касается "интуитивных" решений Настены, то надо отличать необходимый признак сходимости от достаточных
)Поскольку интеграл расходится, то и расходится указанный ряд
Что касается "интуитивных" решений Настены, то надо отличать необходимый признак сходимости от достаточных
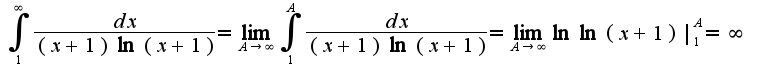
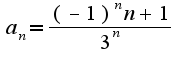 ?
?