Поиск
| Автор | Сообщение |
|---|---|
|
Анна
#
3 апр 2008 |
|
|
О.А.
#
3 апр 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
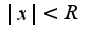 ,где
,где 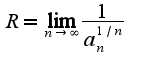 для данного ряда
для данного ряда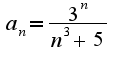 , поэтому
, поэтому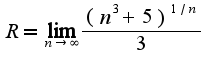 известен предел
известен предел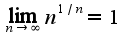 ,поэтому
,поэтому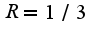 , сл-но,область сходимости
, сл-но,область сходимости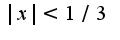 , кроме того, надо провести исследование на концах промежутка,подставив значения в ряд,получим два числовых ряда
, кроме того, надо провести исследование на концах промежутка,подставив значения в ряд,получим два числовых ряда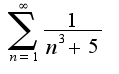
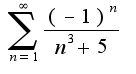 Данные ряды являются сходящимися,первый является обобщенным гармоническим с показателем больше единицы, а второй -ряд Лейбница.Поэтому область сходимости
Данные ряды являются сходящимися,первый является обобщенным гармоническим с показателем больше единицы, а второй -ряд Лейбница.Поэтому область сходимости