Поиск
| Автор | Сообщение |
|---|---|
|
Евгений
#
15 ноя 2006 |
|
|
О.А.
#
15 ноя 2006 |
|
|
WWW
#
19 ноя 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
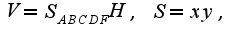 где
где 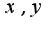 -стороны основания, условия связи между сторонами можно получить из периметра:
-стороны основания, условия связи между сторонами можно получить из периметра: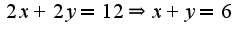 Тогда
Тогда 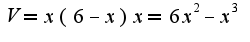 Для нахождения максимума данной функции надо найти первую производную и приравнять нулю, а затем исследовать меняется ли знак у первой производной при переходе через данную стационарную точку.
Для нахождения максимума данной функции надо найти первую производную и приравнять нулю, а затем исследовать меняется ли знак у первой производной при переходе через данную стационарную точку.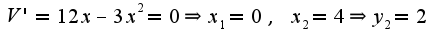 Ясно, что точка максимума:
Ясно, что точка максимума: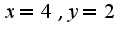 ПРи этом объем
ПРи этом объем 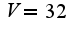 При решении совершенно неважно, какую сторону выбрать в качестве высоты параллелепипеда a или b(можете сами убедиться в этом).
При решении совершенно неважно, какую сторону выбрать в качестве высоты параллелепипеда a или b(можете сами убедиться в этом).