Поиск
| Автор | Сообщение |
|---|---|
|
Аристарх
#
28 ноя 2009 |
|
|
Аристарх
#
28 ноя 2009 |
|
|
О.А.
#
28 ноя 2009 |
|
|
Аристарх
#
28 ноя 2009 |
|
|
Роман
#
2 дек 2009 |
|
|
О.А.
#
2 дек 2009 |
|
|
Роман
#
2 дек 2009 |
|
|
О.А.
#
2 дек 2009 |
|
|
Настя
#
3 дек 2009 |
|
|
О.А.
#
3 дек 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
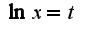 2)
2)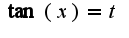 , затем разложение на сумму дробей
3)формула
, затем разложение на сумму дробей
3)формула 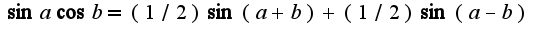 4)выделение полного квадрата, после этого получится табличный интеграл
5)
4)выделение полного квадрата, после этого получится табличный интеграл
5)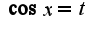
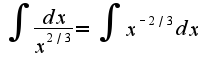 второй пример аналогично
второй пример аналогично