Поиск
| Автор | Сообщение |
|---|---|
|
Полина
#
26 июн 2008 |
|
|
О.А.
#
26 июн 2008 |
|
|
Полина
#
26 июн 2008 |
|
|
Олеся
#
5 мая 2009 |
|
|
Олеся
#
5 мая 2009 |
|
|
О.А.
#
5 мая 2009 |
|
|
Олеся
#
5 мая 2009 |
|
|
О.А.
#
5 мая 2009 |
|
|
Олеся
#
5 мая 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
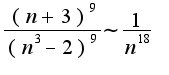 при
при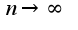 т.к. ряд
т.к. ряд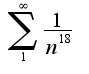 сходится, то сходится исходный
сходится, то сходится исходный
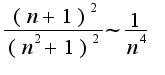 и т.к. этот ряд сходится, то и исходный ряд будет сходиться или я все-таки ошибаюсь?
и т.к. этот ряд сходится, то и исходный ряд будет сходиться или я все-таки ошибаюсь?
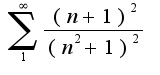
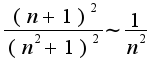 при
при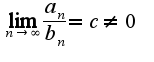 , то из сходимости ряда
, то из сходимости ряда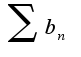 следует сходимость ряда
следует сходимость ряда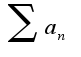 из расходимости ряда
из расходимости ряда