Поиск
| Автор | Сообщение |
|---|---|
|
Дуся
#
30 окт 2007 |
|
|
О.А.
#
30 окт 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
![$ \int_{}{}{\frac{xdx}{\sqrt{x^2+2x+5}}} = \int_{}{}{\frac{xdx}{\sqrt{(x+1)^2+4}}} = [t=x+1; x=t-1; dx=dt] = \int_{}{}{\frac{(t-1)dt}{\sqrt{t^2+4}}} = \frac{1}{2} \int_{}{}{\frac{d(t^2+4)}{\sqrt{t^2+4}}} - \int_{}{}{\frac{dt}{\sqrt{t^2+4}}}= \frac{1}{2}2\sqrt{t^2+4} -ln(t+\sqrt{t^2+4})+C= \sqrt{x^2+2x+5}-ln(x+1+\sqrt{x^2+2x+5})+C$ $ \int_{}{}{\frac{xdx}{\sqrt{x^2+2x+5}}} = \int_{}{}{\frac{xdx}{\sqrt{(x+1)^2+4}}} = [t=x+1; x=t-1; dx=dt] = \int_{}{}{\frac{(t-1)dt}{\sqrt{t^2+4}}} = \frac{1}{2} \int_{}{}{\frac{d(t^2+4)}{\sqrt{t^2+4}}} - \int_{}{}{\frac{dt}{\sqrt{t^2+4}}}= \frac{1}{2}2\sqrt{t^2+4} -ln(t+\sqrt{t^2+4})+C= \sqrt{x^2+2x+5}-ln(x+1+\sqrt{x^2+2x+5})+C$](http://teacode.com/service/latex/latex.png?latex=+%5Cint_%7B%7D%7B%7D%7B%5Cfrac%7Bxdx%7D%7B%5Csqrt%7Bx%5E2%2B2x%2B5%7D%7D%7D+%3D+%5Cint_%7B%7D%7B%7D%7B%5Cfrac%7Bxdx%7D%7B%5Csqrt%7B%28x%2B1%29%5E2%2B4%7D%7D%7D+%3D+%5Bt%3Dx%2B1%3B++x%3Dt-1%3B++dx%3Ddt%5D+%3D+%5Cint_%7B%7D%7B%7D%7B%5Cfrac%7B%28t-1%29dt%7D%7B%5Csqrt%7Bt%5E2%2B4%7D%7D%7D+%3D+%5Cfrac%7B1%7D%7B2%7D+%5Cint_%7B%7D%7B%7D%7B%5Cfrac%7Bd%28t%5E2%2B4%29%7D%7B%5Csqrt%7Bt%5E2%2B4%7D%7D%7D+-+%5Cint_%7B%7D%7B%7D%7B%5Cfrac%7Bdt%7D%7B%5Csqrt%7Bt%5E2%2B4%7D%7D%7D%3D+%5Cfrac%7B1%7D%7B2%7D2%5Csqrt%7Bt%5E2%2B4%7D+-ln%28t%2B%5Csqrt%7Bt%5E2%2B4%7D%29%2BC%3D+%5Csqrt%7Bx%5E2%2B2x%2B5%7D-ln%28x%2B1%2B%5Csqrt%7Bx%5E2%2B2x%2B5%7D%29%2BC&fontsize=21) А вот, что должно получиться:
А вот, что должно получиться:
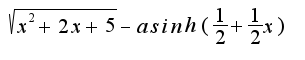 Правильно ли я решила?
Правильно ли я решила?