Поиск
| Автор | Сообщение |
|---|---|
|
Дуня
#
12 ноя 2007 |
|
|
О.А.
#
12 ноя 2007 |
|
|
Дуня
#
12 ноя 2007 |
|
|
О.А.
#
12 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
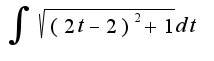 Я пробовала ввести замену:
Я пробовала ввести замену: 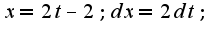
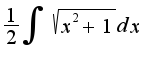 А что теперь с ним делать? Если еще одну замену делать или по частями брать, то этого оказывается недостаточно. Нужно еще упрощать.
Подскажите, пожалуйста, способ.
В справочнике есть готовое решение этого интеграла, но мне нужно самой подробно расписать ход решения.
А что теперь с ним делать? Если еще одну замену делать или по частями брать, то этого оказывается недостаточно. Нужно еще упрощать.
Подскажите, пожалуйста, способ.
В справочнике есть готовое решение этого интеграла, но мне нужно самой подробно расписать ход решения.
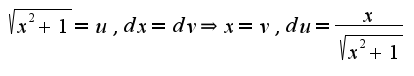 Получим
Получим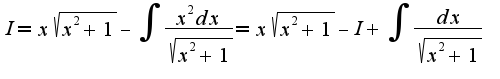 Сл-но,
Сл-но,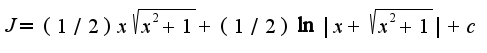
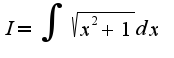 преобразовали числитель-добавляем и вычитаем единицу
преобразовали числитель-добавляем и вычитаем единицу