Поиск
| Автор | Сообщение |
|---|---|
|
Настя
#
17 окт 2008 |
|
|
О.А.
#
17 окт 2008 |
|
|
Настя
#
17 окт 2008 |
|
|
Настя
#
17 окт 2008 |
|
|
О.А.
#
17 окт 2008 |
|
|
Настя
#
17 окт 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
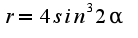 подскажите с границами интегрирования
я начала делать так:
на графике получилось 4 лепестка, можно найти площадь одного и умножить на 4, верно?
а одного:
подскажите с границами интегрирования
я начала делать так:
на графике получилось 4 лепестка, можно найти площадь одного и умножить на 4, верно?
а одного:
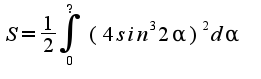 так? толко я незнаю как разобраться с границами
может вообще не так? прошу у вас помощи
так? толко я незнаю как разобраться с границами
может вообще не так? прошу у вас помощи
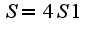 , где
, где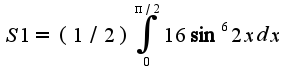
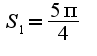 тогда
тогда  ? верно
а почему то в ответах написано
? верно
а почему то в ответах написано 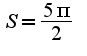 не могли бы вы посчитать, я уже вчера весь вечер считала, сегодня, всё-равно так получается и всё
не могли бы вы посчитать, я уже вчера весь вечер считала, сегодня, всё-равно так получается и всё
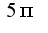 , проверьте еще раз условие, если правильно, то и сомнений быть не должно
, проверьте еще раз условие, если правильно, то и сомнений быть не должно