Поиск
| Автор | Сообщение |
|---|---|
|
Дима
#
26 дек 2005 |
|
|
О.А.
#
26 дек 2005 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
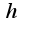 , то для любого действительного числа
, то для любого действительного числа  найдется единственное целое число
найдется единственное целое число 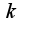 , что выполнится неравенство
, что выполнится неравенство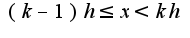 , то доказательство его приведено в учебнике Зорича В.А. Математический анализ, Т.I
, то доказательство его приведено в учебнике Зорича В.А. Математический анализ, Т.I