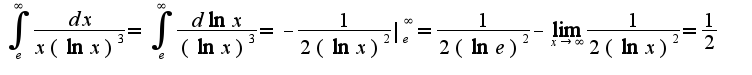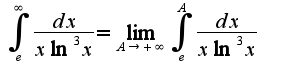Поиск
| Автор | Сообщение |
|---|---|
|
Виталий
#
8 дек 2007 |
|
|
Владимир
#
8 дек 2007 |
|
|
Виталий
#
8 дек 2007 |
|
|
Виталий
#
8 дек 2007 |
|
|
Владимир
#
8 дек 2007 |
|
|
Владимир
#
8 дек 2007 |
|
|
О.А.
#
8 дек 2007 |
|
|
Виталий
#
8 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
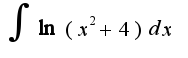 .
.
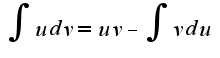 За
За 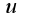 надо принять
надо принять 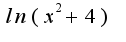 ,
, 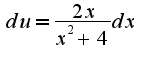 за
за 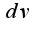 - единицу,
- единицу, 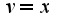 .
Получается
.
Получается 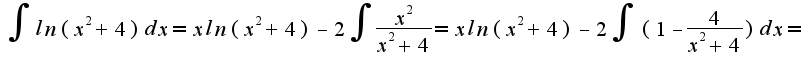
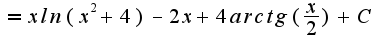
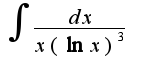
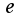 до бесконечности
до бесконечности