Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Поиск| Автор | Сообщение |
|---|---|
|
О.А.
#
11 окт 2009 |
|
|
LOSt
#
11 окт 2009 |
|
|
Арина
#
12 окт 2009 |
|
|
О.А.
#
12 окт 2009 |
|
|
Арина
#
12 окт 2009 |
|
|
валя
#
16 окт 2009 |
|
|
О.А.
#
16 окт 2009 |
|
|
Олег
#
21 окт 2009 |
|
|
Олег
#
21 окт 2009 |
|
|
О.А.
#
21 окт 2009 |
|
|
Македонский
#
21 окт 2009 |
|
|
О.А.
#
21 окт 2009 |
|
|
Антон
#
21 окт 2009 |
|
|
О.А.
#
21 окт 2009 |
|
|
Македонский
#
21 окт 2009 |
Страницы: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
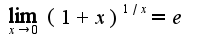
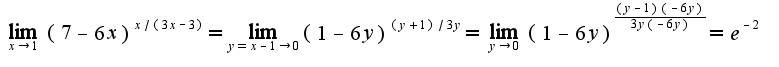
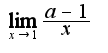
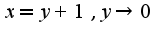 и
и 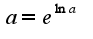
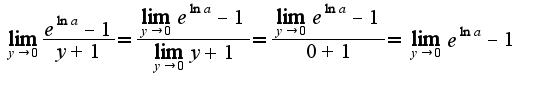 Можно ли теперь воспользоваться заменой эквивалентных бесконечно малых?
Можно ли теперь воспользоваться заменой эквивалентных бесконечно малых?
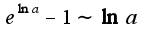 Если да, то получается
Если да, то получается
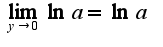 Правильно или нет?
Правильно или нет?
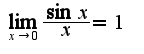
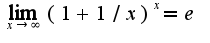
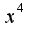 так как степень в знаменателе выше, чем в числителе, то предел равен нулю
так как степень в знаменателе выше, чем в числителе, то предел равен нулю