Поиск
| Автор | Сообщение |
|---|---|
|
Гость
#
19 ноя 2007 |
|
|
О.А.
#
19 ноя 2007 |
|
|
Гость
#
19 ноя 2007 |
|
|
О.А.
#
19 ноя 2007 |
|
|
Гость
#
27 ноя 2007 |
|
|
О.А.
#
27 ноя 2007 |
|
|
Гость
#
27 ноя 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
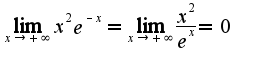
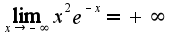
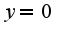 ,т.к.
,т.к.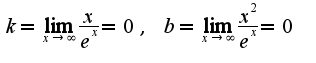 график функции
http://matan.isu.ru/kons22.gif
график функции
http://matan.isu.ru/kons22.gif