Поиск
| Автор | Сообщение |
|---|---|
|
susan
#
24 окт 2013 |
|
|
o.a.
#
24 окт 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
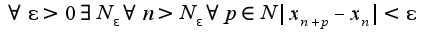 Запишем
Запишем 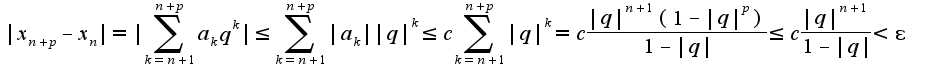 Затем надо решить полученное неравенство относительно
Затем надо решить полученное неравенство относительно 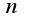 :
: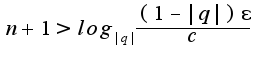
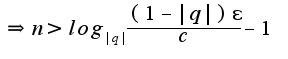 Сл-но, в качестве номера
Сл-но, в качестве номера 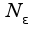 надо выбрать целую часть от полученного номера
надо выбрать целую часть от полученного номера ![$N_{\epsilon}=[log_{|q|}\frac{(1-|q|)\epsilon}{c}-1]$ $N_{\epsilon}=[log_{|q|}\frac{(1-|q|)\epsilon}{c}-1]$](http://teacode.com/service/latex/latex.png?latex=N_%7B%5Cepsilon%7D%3D%5Blog_%7B%7Cq%7C%7D%5Cfrac%7B%281-%7Cq%7C%29%5Cepsilon%7D%7Bc%7D-1%5D&fontsize=21)