Наталья
#
27 мар 2007
|
Здраствуйте, Ольга Александровна. Будьте так добры, проверьте решение.
(а) Написать уравнение касательной плоскости и нормали в точке (x0, y0, f(x,y)) к поверхности S, заданной уравнением z = f(x,y);
(б) Вычислить grad(z) в точке M0(x0,y0);
(в) Вычислить производную функции z = f(x,y) в точке M0(x0,y0) по направлению вектора a.
z = x^2 + xy + y^2, M0(1;1), a = 2i – j
(г) Найти три первых отличных от нуля члена разложения в степенной ряд решения y = y(x) дифференциального уравнения y’ = x + x^2 + y^2, удовлетворяющего начальному условию у(0) = 5
Ответы:
(а) Ур-е касательной -3x – 3y + z + 9 = 0, Ур-е нормали x–1 = y–1 = 3(3-z)
(б) grad(z) = (3,3)
(в) dz/da (1,1) = 9 / 5^1/2
(г) y(x) = 1 +25x + 25x^2+…
|
Ирина
#
7 мая 2007
|
Здраствуйте, Ольга Александровна!
Очень нужна Ваша помощь....зарешалась/обрешалась, в общем одним махом решала контрольную работу...Проверите пожалуйста, верно ли решены задачи.
1)Вычислить двойной интерграл по области D, ограниченной указанными линиями: Двойной интеграл по области D(x^2+y)dxdy, D: y = x^2, x=y^2.
Ответ:у меня получилось интеграл от 0 до 1 dx интеграл от x^2 до корня от x (x^2+y)dy. Вычислила интегралы и получилось 93/140.
2)Вычислить объем тела. Ограниченного поверхностями x^2+y^2=1, z=2-x^2-y^2, z=0.
Ответ:4пи/3
3) Найти наибольше и наименьшее значение функции z=x^2+y^2-xy в квадрате |x|+|y| <=1
Ответ:zmin(0,0) = 0
zmax(-1,1)=3
zmax(1,-1)=3
4)Для уравнения x^2-2*корень из2*x+4=0 найти комплексный корни x1 и x2 (За x1 принять корень с положительной мнимой частью).Для них вычислить
а)x1+x2, x1-x2, x1*x2, x1/x2, x2/x1
б)модуль и аргумент, а также представить x1 и x2 в тригонометрической форме
в)все значения корень х1 и корень х2
Ответ:
a)2*корень из2, 2*корень из2*i,4, i,-i
б) модуль x=2, argx1=пи/4, argx2=-пи/4
в) корень из 2*е^(i*пи/8), корень из 2*е^(i*9*пи/8), корень кубический из 2*е^(-i *пи/12), корень кубический из 2*е^(i*7пи/8), корень кубический из 2*е^(i*15пи/12)
5) найти общее решение дифференциальных уравнений:
а)(1-x^2)y’’=xy’
б)2y’’+(y’)^2+(y’)^4=0
Ответ:
а)y=arcsin(1-x^2)+c
б)y+(y-c)/x+((y-c)/x)^3=0
6) Найти частное решение дифференциального уравнения y’’+py’+gy=f(x), удовлетворяющее начальным условиям y(0)=y0, y’(0)=y’0, p=-4, g=13, f(x)=26x+5,y0=1, y’0=0
Ответ y=-(2/3)*e^(2x)*sin3x+2x+1
7) С помощью характеристического уравнения найти общее решение системы линейных дифференциальных уравнений с постоянными коэффициентами.
Ответ: x=c1e^x+c2e^(-9x), y=-3/4 c1e^x+1/2c2e^(-9x)
8) Всякая касательная к кривой, проходящей через точку А(1;5), отсекает на оси ординат отрезок, равный утроенной абсциссе точки касания. Найти уравнение этой кривой.
Ответ:f(x)=-2x^2+7x
P.S. Очень надеюсь на Вашу помощь
|
Ирина
#
30 мая 2007
|
Здраствуйте, Ольга Александровна!
Проверьте пожалуйста, верно ли решена задачка
2)Вычислить объем тела. Ограниченного поверхностями x^2+y^2=1, z=2-x^2-y^2, z=0.
Ответ:8пи/3...(по другому варианту 10пи/3)...не могу понять, где ошибка...искала не нахожу. Может решение вообще не такое. Помогите пожалуйста. решено это через тройной интеграл(переходя к полярным координатам).
8) Всякая касательная к кривой, проходящей через точку А(1;5), отсекает на оси ординат отрезок, равный утроенной абсциссе точки касания. Найти уравнение этой кривой.
Ответ:f(x)=-2x^2+7x
С нетерпением жду ответа
|
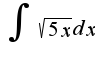 =
=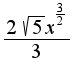
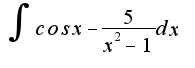 =
=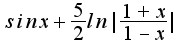
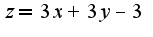 Уравнение нормали правильно записано,градиент верно найден, а производная по направлению определяется по формуле:
Уравнение нормали правильно записано,градиент верно найден, а производная по направлению определяется по формуле: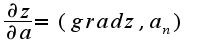 , где
, где 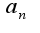 -нормированный вектор,т.е. координаты вектора надо поделить на модуль
-нормированный вектор,т.е. координаты вектора надо поделить на модуль