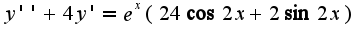Поиск
| Автор | Сообщение |
|---|---|
|
Кирилл
#
17 дек 2007 |
|
|
О.А.
#
17 дек 2007 |
|
|
Кирилл
#
18 дек 2007 |
|
|
О.А.
#
18 дек 2007 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
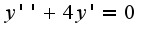 . решая характеристическое уравнение
. решая характеристическое уравнение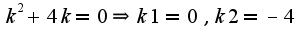 отсюда определяется общее решение, которое имеет вид
отсюда определяется общее решение, которое имеет вид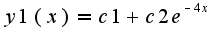 2)ищется частное решение неоднородного уравнения согласно виду правой части и учитывая, что нуль не является корнем характеристического уравнения
2)ищется частное решение неоднородного уравнения согласно виду правой части и учитывая, что нуль не является корнем характеристического уравнения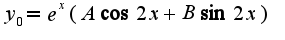 Для определения коэффициентов
Для определения коэффициентов 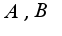 подставляют
подставляют 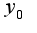 в уравнение, в данном случае
в уравнение, в данном случае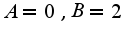 3)теперь можно выписать общее решение неоднородного уравнения, которое является суммой
3)теперь можно выписать общее решение неоднородного уравнения, которое является суммой