Поиск
| Автор | Сообщение |
|---|---|
|
Пермецель
#
6 мар 2009 |
|
|
О.А.
#
7 мар 2009 |
|
|
Пермецель
#
7 мар 2009 |
|
|
О.А.
#
7 мар 2009 |
|
|
Пермецель
#
7 мар 2009 |
|
|
О.А.
#
7 мар 2009 |
|
|
Пермецель
#
9 мар 2009 |
|
|
О.А.
#
9 мар 2009 |
|
|
Пермецель
#
10 мар 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
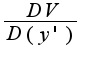 и
и 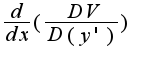 (Здесь D - частная производная)
от выражения
(Здесь D - частная производная)
от выражения ![$ V[y(t)]= \int { \frac {\sqrt{1+(y')^2}} {y}} dx$ $ V[y(t)]= \int { \frac {\sqrt{1+(y')^2}} {y}} dx$](http://teacode.com/service/latex/latex.png?latex=+V%5By%28t%29%5D%3D+%5Cint+%7B+%5Cfrac+%7B%5Csqrt%7B1%2B%28y%27%29%5E2%7D%7D+%7By%7D%7D+dx&fontsize=21)
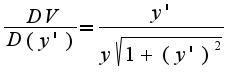
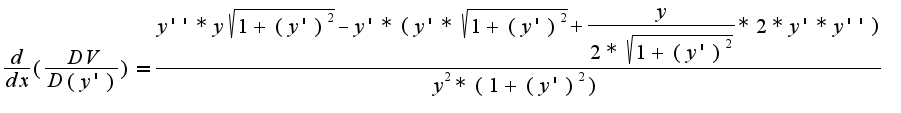 А дальше, если все правильно, то я упрощу выражение.
А дальше, если все правильно, то я упрощу выражение.
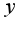 от
от  или
или 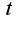 ,в выражении
,в выражении 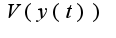 слева функция от
слева функция от ![$ V[y(x)]= \int { \frac {\sqrt{1+(y')^2}} {y}} dx$ $ V[y(x)]= \int { \frac {\sqrt{1+(y')^2}} {y}} dx$](http://teacode.com/service/latex/latex.png?latex=+V%5By%28x%29%5D%3D+%5Cint+%7B+%5Cfrac+%7B%5Csqrt%7B1%2B%28y%27%29%5E2%7D%7D+%7By%7D%7D+dx&fontsize=21) зависит от х, задан функционал
зависит от х, задан функционал
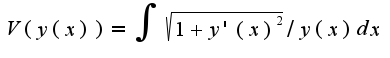 правая часть это число,т.к.
правая часть это число,т.к. 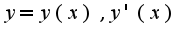 -зависят от
-зависят от 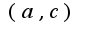 и
и 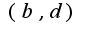 Тогда длина пути
Тогда длина пути 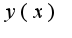 , соединяющего эти точки, может быть записана следующим образом:
, соединяющего эти точки, может быть записана следующим образом:
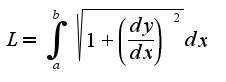 Уравнение Эйлера — Ланранжа для этого функционала принимает вид:
Уравнение Эйлера — Ланранжа для этого функционала принимает вид: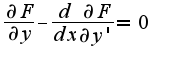 или в подробном виде
или в подробном виде 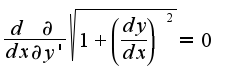 ,
откуда получаем, что
,
откуда получаем, что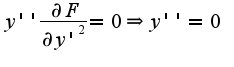
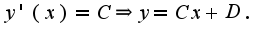 Таким образом, получаем прямую линию. Учитывая, что
Таким образом, получаем прямую линию. Учитывая, что 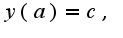
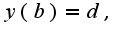 т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.
т. е. что она проходит через исходные точки, получаем верный ответ: отрезок, соединяющий точки.
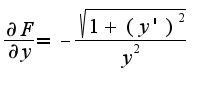 3) находим производную:
3) находим производную: 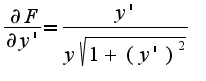 4) находим производную:
4) находим производную: 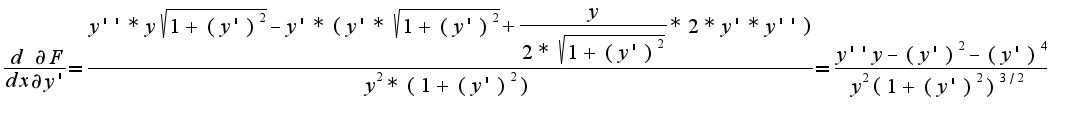 5) подставляем производные в уравнение Эйлера:
5) подставляем производные в уравнение Эйлера: 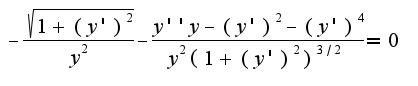
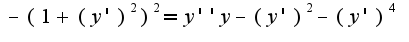
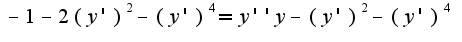
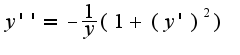 6) решаем диф.уравнение:
6) решаем диф.уравнение:
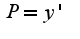 ,
, 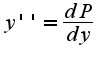
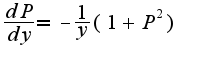
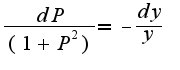
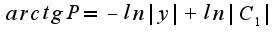
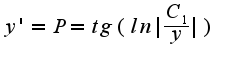 а дальше не решается...
Ответ должен быть таким
а дальше не решается...
Ответ должен быть таким 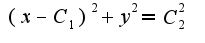 Не пойму, где ошибка.
Не пойму, где ошибка.
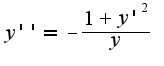 Дальше замена
Дальше замена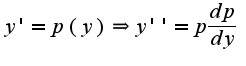 Поэтому у Вас не получается
Поэтому у Вас не получается