Поиск
| Автор | Сообщение |
|---|---|
|
Алиса
#
5 мар 2008 |
|
|
О.А.
#
5 мар 2008 |
|
|
Алиса
#
6 мар 2008 |
|
|
Алиса
#
6 мар 2008 |
|
|
О.А.
#
6 мар 2008 |
|
|
Алиса
#
6 мар 2008 |
|
|
Алиса
#
1 апр 2008 |
|
|
О.А.
#
1 апр 2008 |
|
|
Алиса
#
2 апр 2008 |
|
|
О.А.
#
2 апр 2008 |
|
|
ирина
#
19 ноя 2008 |
|
|
О.А.
#
19 ноя 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
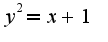
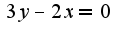
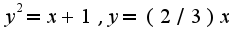 , таким образом узнаете пределы интегрирования, затем удобнее интегрировать по переменной
, таким образом узнаете пределы интегрирования, затем удобнее интегрировать по переменной 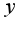
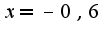 и
и 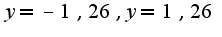
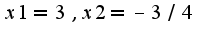
 подставить в любое уравнение.И тогда получатся две точки пересечения.
подставить в любое уравнение.И тогда получатся две точки пересечения.
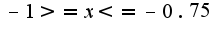 ,вторая фигура в пределах
,вторая фигура в пределах 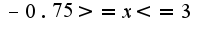 Но почему то площади этих фигур у меня получаются отрицательными,а ведь этого не может быть!
Но почему то площади этих фигур у меня получаются отрицательными,а ведь этого не может быть!
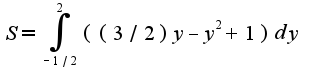
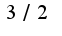 за знак интеграла,получится
за знак интеграла,получится 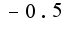 до
до 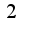 Под интегралом
Под интегралом 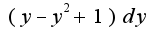 2)начинаем интегрировать,получится
2)начинаем интегрировать,получится 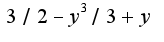 черта от
черта от