Поиск
| Автор | Сообщение |
|---|---|
|
Кристи
#
14 июн 2013 |
|
|
o.a.
#
15 июн 2013 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
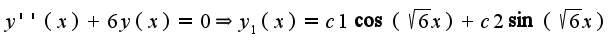 Затем найти частное решение в виде:
Затем найти частное решение в виде: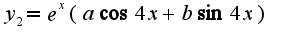 , где
, где 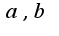 -неопределенные коэффициенты, которые определяются после подстановки в исходное уравнение
-неопределенные коэффициенты, которые определяются после подстановки в исходное уравнение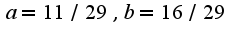 . Общее решение данного уравнение находится как сумма общего решения однородного и частного решения неоднородного.
. Общее решение данного уравнение находится как сумма общего решения однородного и частного решения неоднородного.