Поиск
| Автор | Сообщение |
|---|---|
|
OМГ
#
16 июн 2006 |
|
|
ирина
#
16 июн 2006 |
|
|
О.А.
#
16 июн 2006 |
|
|
ната
#
18 июн 2006 |
|
|
О.А.
#
19 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
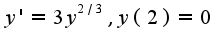
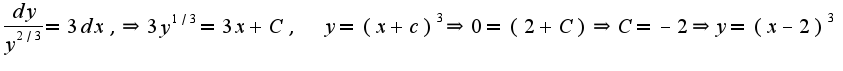 2)
2)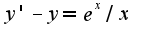 Данное уравнение является линейным, его можно решать методом вариации произвольной константы:
Данное уравнение является линейным, его можно решать методом вариации произвольной константы: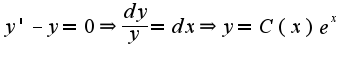 Затем подставить найденное решение однородного уравнения в неоднородное и найти C(x).
Затем подставить найденное решение однородного уравнения в неоднородное и найти C(x). 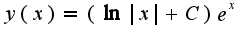
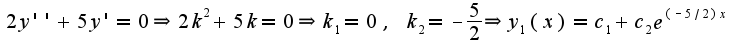 2)затем ищется частное решение неоднородного уравнения по формуле:
2)затем ищется частное решение неоднородного уравнения по формуле: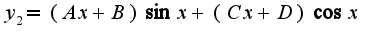 Чтобы найти коэффициенты A,B,C,D подставляют
Чтобы найти коэффициенты A,B,C,D подставляют 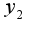 в данное уравнение и приравнивают коэффициенты при
в данное уравнение и приравнивают коэффициенты при 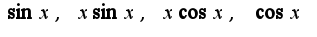
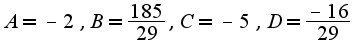 Поэтому решение данного уравнения имеет вид
Поэтому решение данного уравнения имеет вид