Поиск
| Автор | Сообщение |
|---|---|
|
наташа
#
2 июн 2008 |
|
|
О.А.
#
2 июн 2008 |
|
|
наташа
#
3 июн 2008 |
|
|
Купер
#
10 июн 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
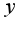 зависит от
зависит от  :
: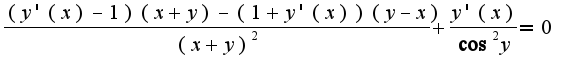 Из полученного уравнения найти производную
Из полученного уравнения найти производную