Поиск
| Автор | Сообщение |
|---|---|
|
6enfant
#
21 янв 2009 |
|
|
6enfant
#
21 янв 2009 |
|
|
О.А.
#
21 янв 2009 |
|
|
6enfant
#
21 янв 2009 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
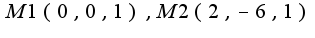 , точка
, точка 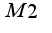 дает минимум, в M1 нет экстремума
дает минимум, в M1 нет экстремума