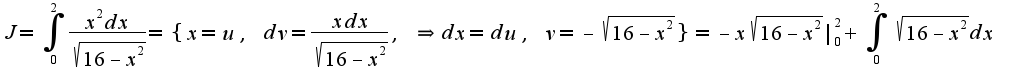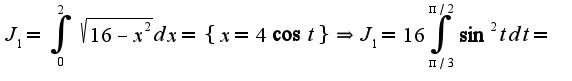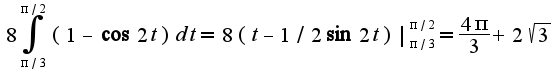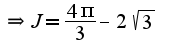Поиск
| Автор | Сообщение |
|---|---|
|
Екатерина
#
21 июн 2006 |
|
|
О.А.
#
22 июн 2006 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
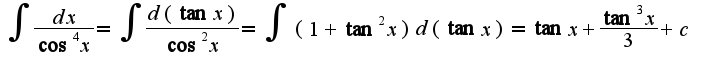 2)
2)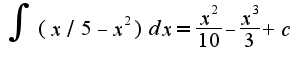 3)Для вычисления используется интегрирование по частям:
3)Для вычисления используется интегрирование по частям: