Поиск
| Автор | Сообщение |
|---|---|
|
Константин
#
12 окт 2008 |
|
|
О.А.
#
12 окт 2008 |
Чтобы написать сообщение, необходимо войти или зарегистрироваться
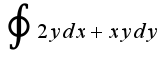 вдоль контура, образованного прямымии
вдоль контура, образованного прямымии 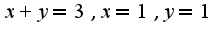 в положительном направлении. Проверить результат с помощью формулы Грина.
Пожалуйста помогите!!! Заранее спасибо!!!
в положительном направлении. Проверить результат с помощью формулы Грина.
Пожалуйста помогите!!! Заранее спасибо!!!
 , что касается формулы Грина, то она следующая:
, что касается формулы Грина, то она следующая: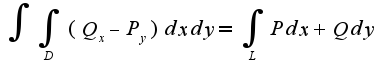 Для данного примера
Для данного примера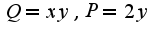 Двойной интеграл
Двойной интеграл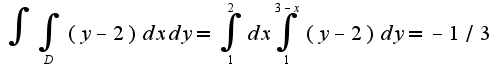 Пределы интегрирования легко установить по картинке
Пределы интегрирования легко установить по картинке